TANTOS EQUIVALENTES EN EXCEL

LEYES FINANCIERAS DE CAPITALIZACION: TANTOS EQUIVALENTES.

Dos tantos cualesquiera, expresados en distintas unidades de tiempo, se dice que son tantos equivalentes cuando aplicados a un mismo capital inicial durante un mismo período de tiempo producen el mismo interés o generan el mismo capital final o montante.

La variación en la frecuencia de cálculo y abono de los intereses obliga a cambiar el tipo de interés a aplicar a la operación para que esta no se vea afectada.

Los tantos equivalentes son proporcionales en Cap. Simple:

i= i_{k *} k

Siendo K la frecuencia de capitalización. K₁₂ sería mensual, K₂ semestral, K₄ trimestral.

Ejemplo

Calcular el montante resultante de invertir 1.000 euros durante 2 años a un tanto de:

Anual 12%

C= 1.000 * (1+ 2 * 0,12) = 1.240

Semestral 6%

C= 1.000 * (1+ 2 * 0,06 * 2) = 1.240

Mensual 1%

C= 1.000 * (1+ 2 * 0,01 * 12) = 1.240

Si mantenemos esta proporcionalidad en la capitalización compuesta por la acumulación de intereses no obtendríamos el mismo capital final. Ejemplo, 1.000 euros al 12% anual dará un capital distino si cambiamos la frecuencia, 6% semestral:

Cn= 1.000* (1+0,12)^1 = 1.120,00

Cn= 1.000* (1+0,06)^2= 1.123,60

Los tantos equivalentes en Cap. Compuesta han de cumplir.

(1+i) = (1+ik)^k

donde K, es la frecuencia de capitalización, que indica:

• El número de partes iguales en que se divide el período que se toma como referencia, normalmente anual.
• Cada cuanto tiempo se acumulan los intereses al capital para calcular nuevos intereses.

En el ejemplo anterior, 1+ 0,12= (1+ i2)^2, donde i2 = 5,83%. Si calculamos Cn =1.000 (1+0,0583)^2= 1.120,00.

Dada las dificultades de aplicación de la formula de relación, se crea un tanto, denominado nominal, proporcional o lineal, que nos permita pasar directamente a un tanto efectivo k-esimal:

Jk = ik * k

Por tanto, definimos:

TASA DE INTERÉS EFECTIVO

Es i o ik. Es la aplicada al final del período para calcular los intereses. Al hacer referencia a una tasa sino se expresa claridad sobre su tipo se dice que esta es efectiva pero si se habla de períodos de capitalización en un futuro o se expresa el término "convertible" esta es nominal.

Para calcular la tasa de interés efectivo en excel,   usaremos la función INT.EFECTIVO cuya sintaxis es (tasa_nominal;num_per_año):

• Int_nominal: Es la tasa de interés nominal del préstamo.
• num_per_año:  Es el número de pagos de interés compuesto por año.

TASA NOMINAL

Es Jk, la tasa que da el punto de partida al análisis financiero, que es teórica y que se utiliza solo para el calculo de la tasa efectiva, ik. Se expresa anualmente y se capitaliza una o varias veces en el año. Si se capitaliza sólo una vez en el año se convierte en la tasa efectiva, pues es la que realmente se paga.

Para calcular la tasa de interés nominal en excel,  emplearemos la función TASA.NOMINAL cuya sintaxis es (tasa_efectiva;num_per):

• Tasa_Efectiva: Es la tasa de interés efectiva anual del préstamo.
• num_per_año:  Es el número de pagos de interés compuesto por año.

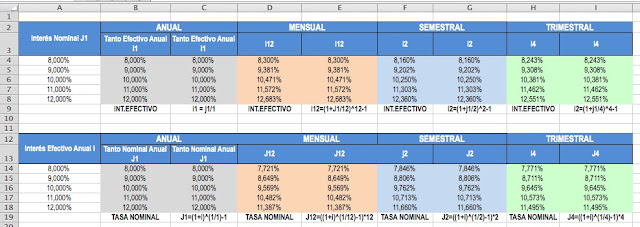
Para entender todos los conceptos se ha creado una tabla de tantos equivalentes. Por un lado partimos de una Tasa Nominal Anual y calculamos a partir de este la Tasa Efectiva Anual, Semestral, Trimestral y Mensual.

Lo más sencillo es utilizar la función INT.EFECTIVO, donde el primer argumento sería la Tasa Nominal y el segundo el período, 1, 2, 4 y 12 respectivamente. También hemos utilizado las correspondientes formulas financieras para obtener el mismo resultado a efectos didácticos.

Por otro lado, se ha partido del Tasa Efectiva Anual para calcular la Tasa Nominal Anual, Semestral, Trimestral y Mensual. Utilizamos la función TASA.NOMINAL, donde el primer argumento es la Tasa Efectiva Anual y el segundo, período, 1, 2, 4 y 12 respectivamente. También hermos realizado los cálculos mediante las formulas financieras para llegar al mismo resultado.

Os adjunto el archivo para que lo podáis descargar: Tabla Tantos Equivalentes

Para verlo aún más claro veamos otro ejercicio:

Tengo una Tasa Anual Efectiva, i, que es del 8%. Calcular el tanto efectivo mensual y el tanto nominal mensual.


Sabemos que (1+i) = (1+im)^m Entonces, i12= (1+0,08)^(1/12)-1= 0,64%. Calculado el tanto efectivo mensual, la Tasa Nominal Mensual sería j12 = i12 *12 =7,72%.


Si los cálculos los realizo en Excel, TASA.NOMINAL(0,08;12) para calcular J12. Calculado este, i12= 7,72/12=0,64%.


Vamos a suponer ahora que el valor que conozco es el Tanto Efectivo Mensual, i12, que es del 1%.


El tanto efectivo anual, sería i= (1+0,01)^12 - 1= 12,68%. J12= 1%*12 = 12%. En Excel,  J12 sería igual a  i12*12= 12%. La Tasa Efectiva Anual, i, será INT.EFECTIVO(0,12;12)= 12,68%.


Supongamos ahora que tenemos J12 que es del 12%. I12 será= 12/12 = 1% y la tasa efectiva anual, i=(1+0,01)^12 - 1= 12,68%. En Excel, i12 será= 12/12 = 1%  e i será será INT.EFECTIVO(0,12;12)= 12,68%.


Por último, si tengo que el Tanto Efectivo Semestral del 6%, i2, vamos a calcular el tanto efectivo mensual, i12, sin necesidad de calcular previamente el Tanto Efectivo Anual:


i12= (1+0,06)^(1/6) -1 = 0,98%. El razonamiento es que en un semestre hay seis meses, por tanto partiendo de i2, que es el período más grande y como si fuera i, calculamos i12.

Respecto a la modalidad de las tasas, es decir al momento en que se pagan los intereses, si es al principio del período, sería anticipado o prepagable, y si es al final del período, sería vencido o pospagable. La relación entre ambas tasas es la siguiente en capitalización compuesta:

ï = i / (1+ i) o bien

i = ï / (1- ï)


o en capitalización simple:


ï = i / (1+ n * i) o bien


i = ï / (1 -n* ï)

donde i es pospagable e ï prepagable. Veamos unos ejemplos:


Calcular en capitalización simple el ahorro obtenido de invertir 1.000 euros al 10% de interés anual prepagable y durante un año:


Cn = 1.000 * (1- 0,10*1) = 90.000.  El interés pospagable sería. 0,10/ (1-0,10) = 11,11%.


Realizar el mismo calculo pero en capitalización compuesta.


Cn= 1.000 * (1-0,10)^1 = 90.000 El interés pospagable: 0,10/ 0,90 = 11,11%

 Suscríbete y recibe por mail los artículos

Imprimir artículo

---

Si te gustó el artículo puedes agregar mi blog en tu iGoogle o Yahoo, Gracias.

Comparte esta entrada

Tweet

---

NOTA:Si has encontrado útil este artículo puedes compartirlo en las Redes Sociales pulsando el botón anterior y/o puedes copiar estos links para compartirlo desde tu blog, página Web o foro.

URL:

Link HTML:

Link para foros: