Inicio
Autor
Excel
Gestión
Operaciones Financieras
Presupuestos
Costes
Cuadros de Mando
Análisis Económico-Financiero
Reporting
Planes de Negocios
Físcal
Contactar
Contactar
Suscripción
Artículos
EQUIVALENCIA DE CAPITALES. RESERVA MATEMÁTICA.
La equivalencia financiera consiste en igualar los capitales de la prestación con las de la contraprestación valorados todos ellos en el mismo instante de tiempo t.
Veamos un ejercicio para entender el concepto. Supongamos que tenemos una Prestación formada por los siguientes capitales: En los años 0 1.000€, 1 1.200€ y 3 1.500. Por otra parte, una Contraprestación formada por los capitales 500€ en el segundo año, 1.600€ en el tercer año y un capital X en el cuarto. Pues bien, el problema es calcular X de tal forma que ambas operaciones sean equivalentes financieramente. La tasa de interés efectiva anual es del 10%.
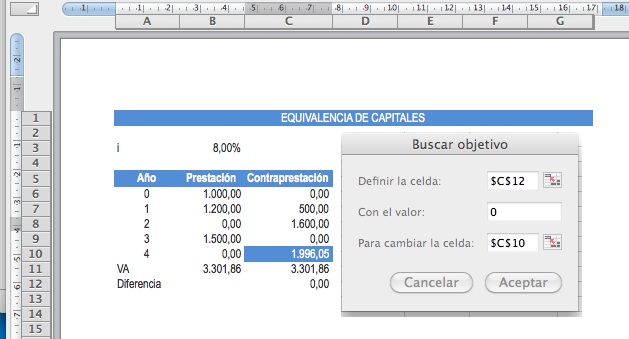
Para la resolución del problema creamos una tabla con las columnas años, prestación y contraprestación. Pues bien, calculamos el VA de la prestación y contraprestación, en este caso sería, VNA(B3;B7:B10)+B6 para la prestación, al ser prepagable le sumamos el primer término en cero, B6. Para la contraprestación será VNA(B3;C7:C10)+C6. Por último en la celda C12 indicamos la diferencia. Si hubiera equivalencia de capitales esta diferencia debería ser cero, pero en este caso la celda C10 está vacía, y por tanto la diferencia no es cero. Para calcular el valor del capital en C10 que resuelva la equivalencia financiera utilizaremos SOLVER o BUSCAR OBJETIVO: Datos/Análisis de datos/Buscar Objetivo.
Indicamos en Definir Celda C12, que es donde tenemos la formula de la diferencia, B11-C11. Con el valor, se ha de indicar cero. Para cambiar la celda, indicamos la celda donde indicaremos el capital que necesitamos calcular, C10. Nos dará como resultado un importe de 1.996,05€, que es el importe que hace equivalentes ambos capitales.
Otra forma de resolver el ejercicio planteado es mediante el concepto de Saldo Financiero o Reserva Matemática, en la que podemos distinguir, por un lado, la Reserva por la Izquierda, R-, que es el saldo en ese punto, Prestación menos Contraprestación, sin considerar el saldo que vence en ese instante, y por otro lado, la Reserva por la Derecha, R+, que si considera la cuantía que vence en ese instante.
En nuestra tabla creamos la columna D Saldo Neto que es la diferencia entre la Prestación y la Contraprestación, así en D6=B6-C6 y arrastramos la celda para el resto de la columna. Por otro lado creamos las columnas Reserva por la Izquierda y Derecha. En esta segunda, F6 será el Saldo por la Izquierda, E6, que al inicio es cero, más el sado neto D6. Arrastramos esta celda al resto de la columna. La última celda, F10, el saldo final también si se cumple la equivalencia de capitales debe ser cero. La Reserva por la izquierda, en el año 1, E7, debe ser el saldo del año anterior, F6 capitalizado un período, F6* (1+$B$3). Arrastramos esta formula al resto de la columna. Pues bien, ahora emplearemos Buscar Objetivo, de tal forma, que lo que queremos es que definida la celda F10 con saldo cero nos dé el capital en C10 y aceptamos. De esta forma calcularemos el capital que hace equivalente la prestación y contraprestación.
Para la resolución del problema creamos una tabla con las columnas años, prestación y contraprestación. Pues bien, calculamos el VA de la prestación y contraprestación, en este caso sería, VNA(B3;B7:B10)+B6 para la prestación, al ser prepagable le sumamos el primer término en cero, B6. Para la contraprestación será VNA(B3;C7:C10)+C6. Por último en la celda C12 indicamos la diferencia. Si hubiera equivalencia de capitales esta diferencia debería ser cero, pero en este caso la celda C10 está vacía, y por tanto la diferencia no es cero. Para calcular el valor del capital en C10 que resuelva la equivalencia financiera utilizaremos SOLVER o BUSCAR OBJETIVO: Datos/Análisis de datos/Buscar Objetivo.
Indicamos en Definir Celda C12, que es donde tenemos la formula de la diferencia, B11-C11. Con el valor, se ha de indicar cero. Para cambiar la celda, indicamos la celda donde indicaremos el capital que necesitamos calcular, C10. Nos dará como resultado un importe de 1.996,05€, que es el importe que hace equivalentes ambos capitales.
Otra forma de resolver el ejercicio planteado es mediante el concepto de Saldo Financiero o Reserva Matemática, en la que podemos distinguir, por un lado, la Reserva por la Izquierda, R-, que es el saldo en ese punto, Prestación menos Contraprestación, sin considerar el saldo que vence en ese instante, y por otro lado, la Reserva por la Derecha, R+, que si considera la cuantía que vence en ese instante.
En nuestra tabla creamos la columna D Saldo Neto que es la diferencia entre la Prestación y la Contraprestación, así en D6=B6-C6 y arrastramos la celda para el resto de la columna. Por otro lado creamos las columnas Reserva por la Izquierda y Derecha. En esta segunda, F6 será el Saldo por la Izquierda, E6, que al inicio es cero, más el sado neto D6. Arrastramos esta celda al resto de la columna. La última celda, F10, el saldo final también si se cumple la equivalencia de capitales debe ser cero. La Reserva por la izquierda, en el año 1, E7, debe ser el saldo del año anterior, F6 capitalizado un período, F6* (1+$B$3). Arrastramos esta formula al resto de la columna. Pues bien, ahora emplearemos Buscar Objetivo, de tal forma, que lo que queremos es que definida la celda F10 con saldo cero nos dé el capital en C10 y aceptamos. De esta forma calcularemos el capital que hace equivalente la prestación y contraprestación.
Si te gustó el artículo puedes agregar mi blog en tu iGoogle o Yahoo, Gracias.
Comparte esta entrada
NOTA:Si has encontrado útil este artículo puedes compartirlo en las Redes Sociales pulsando el botón anterior y/o puedes copiar estos links para compartirlo desde tu blog, página Web o foro.
Escribe tu comentario
Publicar un comentario
Tu comentario es IMPORTANTE, son bienvenidos y serán todos respondidos:
1.-Por favor, expresate lo más claro y correcto que puedas, así será todo mucho más fácil. Recuerda puedes contactar conmigo para tratar cualquier duda.
2.-No se permiten descalificaciones y ni faltas de respeto a ningún usuario. Estos comentarios serán automáticamente borrados.
Gracias por vuestra comprensión.