RENTA EN PROGRESION GEOMETRICA PERPETUAS
En este caso el número de términos, n, tiende a infinito. Solo tiene sentido financiero si q, valor del incremento de las rentas en progresión geometrica, es menor que 1+ i.
Valor Actual Valoración de los términos en el origen de la renta.
En excel creamos la función VAgeop(C,q,i), tal y como detallamos para la pospagable:
'VA Valor Actual Renta Variable en Progresión Geometrica Perpetua Pospagable
Function VAgeop(C, q, i) 'Argumentos, C Capital, i tasa interés,q razón de la progresión
VAgeop = C / (1 + i - q)
End Function
Y para la prepagable Vägeop(C,q,i) tal y como se detalla:
'VA Valor Actual Renta Variable en Progresión Geometrica Perpetua Prepagable
Function Vägeop(C, q, i) 'Argumentos, C Capital, i tasa interés,q razón de la progresión
Vägeop = (C / (1 + i - q)) *(1+i)
End Function
Function VAgeop(C, q, i) 'Argumentos, C Capital, i tasa interés,q razón de la progresión
VAgeop = C / (1 + i - q)
End Function
Y para la prepagable Vägeop(C,q,i) tal y como se detalla:
'VA Valor Actual Renta Variable en Progresión Geometrica Perpetua Prepagable
Function Vägeop(C, q, i) 'Argumentos, C Capital, i tasa interés,q razón de la progresión
Vägeop = (C / (1 + i - q)) *(1+i)
End Function
RENTA EN PROGRESION GEOMETRICA DIFERIDAS
Valoradas con anterioridad a su origen. El período de tiempo que transcurre desde el origen al momento de valoración se denomina período de diferimiento, d.
Para valorar la renta, la valoramos a su origen y luego descontamos hasta el momento t elegidos mediante el descuento compuesto al tanto de interés vigente durante el período de diferimiento.
Valor Actual Valoración de los términos en el origen de la renta para después descontarlos al momento t.
En excel, el VA lo podemos calcular de tres formas, bien descontando el VNA (Tasa;Valores), VNA * (1+i)^-d o bien calculando el VNA al origen y que este valor sea el VF del VA al momento del diferimiento, VA(Tasa;nper(d);0;-VNA(Tasa;Valores);0) y donde el pago es igual a cero, o bien creando nuestra propia función, VAgeod(C,q,n,d,i) o Vägeod (C,q,n,d,i) según sea pospagable o prepagable:
'VA Valor Actual Renta Variable Pospagable Temporal Inmediata Entera En Progresión Geometrica caso General y Particular Diferida
Function VAgeod(C, q, n, d, i) 'Argumentos Capital, razón incremento, períodos, diferimiento,tasa interés
If q = 1 + i Then 'Si la condición se cumple
VAgeod = (n * C / (1 + i)) * (1 + i) ^ (-d)
Else 'En caso contrario
VAgeod = (C * (1 - (q / (1 + i)) ^ n) / (1 + i - q)) * (1 + i) ^ (-d)
End If
'VA Valor Actual Renta Variable Prepagable Temporal Inmediata Entera En Progresión Geometrica caso General y particular Diferida
Function Vägeod(C, q, n, d, i) 'Argumentos Capital, razón incremento, períodos, diferimiento, tasa interés
If q = 1 + i Then 'Si la condición se cumple
Vägeod = ((n * C / (1 + i)) * (1 + i)) * (1 + i) ^ (-d)
Else 'En caso contrario
Vägeod = ((C * (1 - (q / (1 + i)) ^ n) / (1 + i - q)) * (1 + i)) * (1 + i) ^ (-d)
End If
End Function
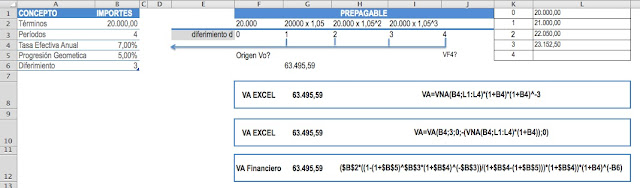
En el siguiente cuadro tenemos una renta diferida prepagable variable en progresión geométrica al 5%. Se puede observar que se calcula el VA descontando el período d o bien calculando el VA del VNA durante el período d:
Valor Final Se calcula como en una renta inmediata ya que el diferimiento sólo afecta al valor actual.
'VA Valor Actual Renta Variable Pospagable Temporal Inmediata Entera En Progresión Geometrica caso General y Particular Diferida
Function VAgeod(C, q, n, d, i) 'Argumentos Capital, razón incremento, períodos, diferimiento,tasa interés
If q = 1 + i Then 'Si la condición se cumple
VAgeod = (n * C / (1 + i)) * (1 + i) ^ (-d)
Else 'En caso contrario
VAgeod = (C * (1 - (q / (1 + i)) ^ n) / (1 + i - q)) * (1 + i) ^ (-d)
End If
'VA Valor Actual Renta Variable Prepagable Temporal Inmediata Entera En Progresión Geometrica caso General y particular Diferida
Function Vägeod(C, q, n, d, i) 'Argumentos Capital, razón incremento, períodos, diferimiento, tasa interés
If q = 1 + i Then 'Si la condición se cumple
Vägeod = ((n * C / (1 + i)) * (1 + i)) * (1 + i) ^ (-d)
Else 'En caso contrario
Vägeod = ((C * (1 - (q / (1 + i)) ^ n) / (1 + i - q)) * (1 + i)) * (1 + i) ^ (-d)
End If
End Function
En el siguiente cuadro tenemos una renta diferida prepagable variable en progresión geométrica al 5%. Se puede observar que se calcula el VA descontando el período d o bien calculando el VA del VNA durante el período d:
Valor Final Se calcula como en una renta inmediata ya que el diferimiento sólo afecta al valor actual.
RENTA EN PROGRESION GEOMETRICA ANTICIPADAS
Se valoran con posterioridad a su final, siendo el período de anticipación, h, el que transcurre entre el final y el momento de su valoración.
Para su valoración, calculamos el VF como en una renta inmediata y lo capitalizamos hasta el momento de su valoración h. También podemos calcular el VA al origen y capitalizarlo hasta el momento de su valoración, h.
El valor actual no se ve afectado, se calcula como el de una renta inmediata.
En excel, calculamos el VF de una Renta Variable en Progresión Geométrica Pospagable o Prepagable. Una vez obtenido este será el VA a indicar en la formula VF donde el período sería h, VF(tasa;nper(h);0;´VF;0), o bien creando nuestra propia función VFgeoh(C, q, n, h, i) ó Vfägeoh(C, q, n, h, i)
'VF Valor Final Renta Variable Pospagable Temporal Inmediata Entera En Progresión Geometrica Anticipada
Function VFgeoh(C, q, n, h, i) 'Argumentos Capital, razón incremento, períodos, período de anticipación, tasa interés
VFgeoh = (VAgeo(C, q, n, i) * (1 + i) ^ n) * (1 + i) ^ h
End Function
'VF Valor Final Renta Variable Prepagable Temporal Inmediata Entera En Progresión Geometrica Anticipada
Function Vfägeoh(C, q, n, h, i) 'Argumentos Capital, razón incremento, períodos, período anticipación, tasa interes
Vfägeoh = (Vägeo(C, q, n, i) * (1 + i) ^ n) * (1 + i) ^ h
End Function
En excel, calculamos el VF de una Renta Variable en Progresión Geométrica Pospagable o Prepagable. Una vez obtenido este será el VA a indicar en la formula VF donde el período sería h, VF(tasa;nper(h);0;´VF;0), o bien creando nuestra propia función VFgeoh(C, q, n, h, i) ó Vfägeoh(C, q, n, h, i)
'VF Valor Final Renta Variable Pospagable Temporal Inmediata Entera En Progresión Geometrica Anticipada
Function VFgeoh(C, q, n, h, i) 'Argumentos Capital, razón incremento, períodos, período de anticipación, tasa interés
VFgeoh = (VAgeo(C, q, n, i) * (1 + i) ^ n) * (1 + i) ^ h
End Function
Function Vfägeoh(C, q, n, h, i) 'Argumentos Capital, razón incremento, períodos, período anticipación, tasa interes
Vfägeoh = (Vägeo(C, q, n, i) * (1 + i) ^ n) * (1 + i) ^ h
End Function
Siguiendo con el ejemplo ya visto, vemos que al cálculo del VA no le afecta y lo calculamos como en un renta inmediata en progresión geometrica, en ese caso prepagable.
Con respecto al VF, por formulas financieras capitalizamos el VA al momento n+h. En Excel, lo podremos hacer de tres formas, una capitalizando al momento n+h el VA de una renta inmediata prepagable en progresión geométrica, o bien, una vez obtenido el VA de la renta inmediata prepagable en progresión geométrica, calcular su VF, donde el pago es cero. Una vez obtenido el valor, calcular el VF para el período h utilizando como VA el VF obtenido anteriormente y el pago 0. Por último, podríamos haber utilizado las funciones creadas que darían el mismo resultado.
Comparte esta entrada
NOTA:Si has encontrado útil este artículo puedes compartirlo en las Redes Sociales pulsando el botón anterior y/o puedes copiar estos links para compartirlo desde tu blog, página Web o foro.



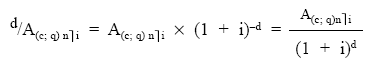


Escribe tu comentario
Publicar un comentario
Tu comentario es IMPORTANTE, son bienvenidos y serán todos respondidos:
1.-Por favor, expresate lo más claro y correcto que puedas, así será todo mucho más fácil. Recuerda puedes contactar conmigo para tratar cualquier duda.
2.-No se permiten descalificaciones y ni faltas de respeto a ningún usuario. Estos comentarios serán automáticamente borrados.
Gracias por vuestra comprensión.